液压缸上总是连着油管的,为此在分析液压缸动态特性时,要使用如图12—3所示的简图。为了简化分析,假定液压缸回油腔直通油箱,而且进油管较短,只需考虑其容积的影响。
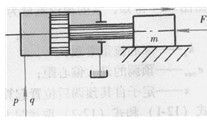
网12-3带管道的液压缸
活塞上的受力方程为
AP=mdv/dt+Bv+FL
式中
A-活塞有效工作面积;
p-液压缸工作腔压力;
Ap(s)=(,ms+B)v(s)+ FL(S)
q(s)=Av(s)+(k1+V/KS)p(s)
由式(12—10)和式(12 -11)可作出带管道的液压缸的框图(见图12—4),并综合成下式
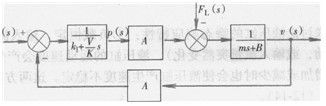
v(s)Aq(s)-(k1+V/Ks)FL(s)/V/Kms2+(k1m+V/KB)s+(A2+k1B)
=1/A2+k1BAq(s)-(k1+V/Ks)FL(S)/s2/ωn2+2ζn/ωns+1
外负载FL恒定(即FL(s)=O)时的液压缸传递函数为
φ1(s)=v1(s)/q(s)=(A/A2+k1B)1/(s/ωn)+2ζn/ωns+1
输人流量q恒定(即q(s)=0)时的液压缸传递涵数为
φ2(s)=v2(s)/FL(S)=(-1/A2+k1B)k1+V/Ks/(s/ωn)2+2ζn/ωns+1
以卜三式中的m。和f。分别代表带管道的液压缸的固有角频率和阻尼比,其表达式为
ωn=√(A2+k1B)K/Vm
ζn=ωn/2Kk1m+VB/A2+k1B
由以上的一些图和公式可以看到:
v1(s)=φ1(s)q(s)=φ1(s)q0/s
也即
v1(s)=Aq0/A2+k1Bs(s2+2ζnωn+ωn2)
v1(t)=Aq0/A2+k1B﹛1-1/√1-ζn2e-ζnωntsin[ωn√1-ζn2t+arctan√1-ζn2/ζn]﹜
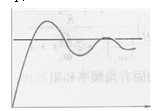
其特性如图12-5a所示。从图中可看出,速度v1围绕稳态值v10I下波动,并逐渐衰减趋向于稳态值。阻尼比ζn越大,则波动越小。由式( 12-17),t=0时,v1=0;t=∞,v1=v10=Aq0/A2+k1B

分类:液压行业知识
标签: 液压马达

